Introduzione
Cos'è
l'architettura
liquida? Quale è la sua essenza?
Mi
ero
già imbattuta inconsapevolmente in architetture che
possono
appartenere a questa “etichetta”, senza realizzare
quanto fossero
completamente frutto del proprio tempo. Ad
incuriosirmi
particolarmente era il senso di spaesamento,
estraniamento, quasi
fastidio, come un prurito interno inspiegabile che
provocava in molte
persone il solo trovarsi di fronte a queste
architetture, dalle
sembianze mostruose, costituite sulla complicata
geometria frattale,
composte da labirinti cervellotici e superfici
riflettenti.
Già
Bruno
Zevi lamentava la mancanza in architettura di un
linguaggio che
fosse diverso da quello classico, così facilmente
comprensibile e
digeribile agli occhi di tutti, abituati alle regole
della simmetria,
della geometria e dell'ordine.
Allora
quale
è il linguaggio dell'architettura contemporanea, che
esprime
realmente qualcosa del suo tempo e non frutto del
rimaneggiamento di
linguaggi passati ormai arcaici e desueti? La
risposta è nel
“liquido”. Liquido, che come Bauman
insegna, è il solo vero aggettivo da abbinare
all'odierna società,
così incline al cambiamento, abituata all'incessante
trasformazione.
Basti
vedere il particolare periodo storico che stiamo
attraversando,
afflitti da una pandemia mondiale, in cui la parola
“certezza”
avanza claudicante, a fatica.
Sfogliando
poi
le pagine dell'Enciclopedia
delle
arti contemporanee
a cura di Achille Bonito Oliva. in particolar modo
il volume che fa
riferimento al tempo
inclinato,
ovvero il tempo della magnifica scoperta di Albert
Einstein, che ha
dato il via nell'arte alle più grandi
sperimentazioni
avanguardistiche, mi sono imbattuta in
un'architettura veramente
singolare di Peter Eisenmann, la Max
Reinhardt
Haus.
Ecco, qui si faceva riferimento esplicito al nastro
di
Möbius.
Spinta dalla curiosità ho iniziato ad “indagare”.
Il
nastro
di Möbius
esprime perfettamente (metaforicamente) il concetto
di spazio-tempo
espresso da Albert Einstein nella legge della
Relatività. Il dentro
e il fuori sono perennemente legati, così come lo
spazio e il tempo
non possono essere pensati separatamente. Non solo,
è anche simbolo
di continua trasformazione, proprio perché essendo
una superficie ad
una sola faccia, percorrendo idealmente la sua
superficie da un punto
X, e attraversando la stessa, si ritorna sempre a
quel punto X di
partenza.
Mi
è
sembrata così una figura estremamente moderna,
qualcosa di
lontano dalle semplici figure geometriche che
conosciamo, qualcosa
che possa essere ben espresso attraverso la
lavorazione tramite
programmi al computer, per la creazione di
un'architettura
veramente contemporanea.
Il
foglio
di carta e la penna tipici dell'architetto hanno
lasciato
spazio al cyberspace,
termine estremamente caro a Marcos Novak.
L'intento
di
questo lavoro è dunque quello di elevare il nastro
di Möbius
e più in generale la topologia a chiave ermeneutica
(una fra le
molte) dell'architettura liquida.
La
ricerca
è soltanto frutto di un'osservazione, così come
soltanto
un'osservazione è stata la scoperta del nastro di Möbius
da parte di August Ferdinand Möbius.
Il
nastro di
Möbius
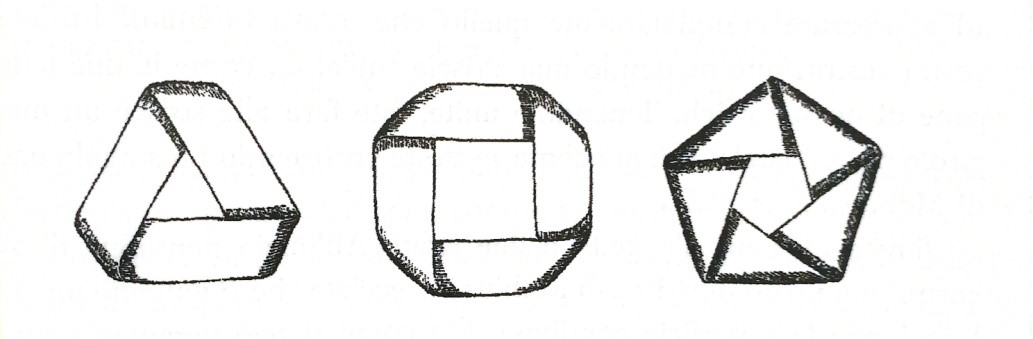 Fig. 1 - Il nastro di Möbius e alcuni suoi parenti con torsioni
Fig. 1 - Il nastro di Möbius e alcuni suoi parenti con torsioni
L'
Enciclopedia
Treccani descrive il Nastro di Möbius
come «superficie
rigata
non orientabile, con una sola faccia e un solo bordo
e,
pertanto, con caratteristica di Eulero. Può essere
ottenuto a
partire da un foglio rettangolare ABCD: si effettua
una torsione di
180° del lato AB e lo si porta a coincidere con il
lato CD, in modo
che il punto A si identifichi con il punto D e il
punto B si
identifichi con il punto C» .
Questa
figura
topologica
ha da sempre affascinato sia matematici, sia lettori
non
specializzati. Con il trascorrere degli anni la
popolarità e le
applicazioni del nastro sono cresciute e oggi esso è
entrato a far
parte a buon diritto della matematica, della magia,
della
letteratura, della musica e dell'arte. È divenuto
una metafora del
cambiamento, dell'insolito, dell'iterazione e del
rinnovamento.
In effetti, ai giorni nostri è utilizzato come
simbolo del riciclo
in quanto rappresenta il processo di trasformazione
dei materiali di
rifiuto in risorse utili, quasi una trasposizione
grafica del «Nulla
si
crea, nulla si distrugge, tutto si trasforma» .
Il
simbolo
del riciclo fu progettato nel 1970 da Gary Anderson,
uno
studente della Southern California University a Los
Angeles, il quale
partecipò con il suo logo a un concorso nazionale
sponsorizzato
dalla Cointaner Corporation of America .
Aion
(in greco: Αἰών) è una divinità ellenistica
associata al tempo
illimitato, all'eternità, in contrasto con Chronos,
che
rappresenta invece il tempo che scorre, diviso in
passato, presente e
futuro. In questo mosaico, oltre alla figura di
Aion, troviamo il
tempo che scorre, rappresentato dalle quattro
stagioni che circondano
Tellus, dea romana della terra, protettrice della
fecondità e dei
morti .
 Fig. 2 - Mosaico Aìon e Lo Zodiaco,
Fig. 2 - Mosaico Aìon e Lo Zodiaco,
Sassoferrato, III secolo d. C, oggi Gliptoteca di Monaco di Baviera
 Fig. 3 - Un ouroboros
Fig. 3 - Un ouroboros
dalla Chrysopoeia di Cleopatra, III d.C. ca.
Venezia, Biblioteca Nazionale Marciana
gr. 299 (= Collocazione 584), XI-XII sec. d.C.
Ma
dunque
gli artisti avevano ben chiare le implicazioni
topologiche? Forse è solo un caso, potremmo
parlare di topologia ante
litteram.
D'altronde la scoperta di Möbius, come abbiamo
asserito diverse
volte, è frutto di una semplice osservazione,
niente di più.
Max
Bill
Le
proprietà
di Möbius
tuttavia,
hanno sedotto molti personaggi del mondo
dell'arte.
Il
famoso
pittore, grafico e scultore Max Bill ha iniziato
a realizzare
nastri senza fine. Lo racconta nel suo articolo
del 1972
Come cominciai a fare le superfici ad una
faccia unica:
«Marcel
Breuer,
il mio vecchio amico della Bauhaus, è il vero
responsabile
delle sculture ad una faccia sola. Ecco come
accade fu nel 1935 a
Zurigo, dove insieme a Emil e Alfred Roth stava
costruendo le case di
Doldertal che ai loro tempi ebbero grande
seguito. Un giorno Marcel
mi disse di aver ricevuto l'incarico di
costruire, per una mostra a
Londra, un modello di casa, dove tutto, perfino
il camino, doveva
essere elettrico. Ci era ben chiaro che un
camino elettrico che
splende ma non ha fuoco non è un oggetto dei più
attraenti.
Cominciai a cercare una soluzione, una struttura
che si potesse
appendere sopra ad un caminetto e che magari
girasse nella corrente
d'aria ascendente, e grazie alla sua forma e al
movimento, agisse
come sostituto delle fiamme. L'arte invece del
fuoco! Dopo lunghi
esperimenti trovai una soluzione che mi sembrava
ragionevole» .
 Fig. 4 - Max Bill, Nastro senza fine, Anversa 1953-56
Fig. 4 - Max Bill, Nastro senza fine, Anversa 1953-56
Bill
stesso
scrive: «Sin
dagli
anni Quaranta pensavo ai problemi di topologia.
Da essi
sviluppai una specie di logica della forma. Le
ragioni per cui venivo
attratto da questo tema particolare sono due: 1)
l'idea di una
superficie infinita (che è tuttavia finita) e
l'idea di un
infinito finito; 2) la possibilità di sviluppare
superfici che, come
conseguenza delle leggi intrinseche , portino
quasi inevitabilmente a
formazioni che provano l'esistenza di una realtà
estetica. Ma sia
1) che 2) indicavano anche un'altra direzione.
Se le strutture
topologiche esistessero solo in virtù della loro
realtà estetica,
allora nonostante la loro esattezza, non avrei
potuto esserne
soddisfatto. Sono convinto che il fondamento
della loro efficacia
stia in parte nel loro valore simbolico; essi
sono modelli per la
riflessione e la contemplazione».
René
Huyghe,
dell'Accadémie Francaise, nel suo libro Formes
et
Forces: de l'atome à Rembrandt
ha dedicato un capitolo intero al tema della
continuità e
discontinuità, con precisi riferimenti alla
topologia nell'arte
contemporanea: «Pertanto
la
scienza, dagli inizi del ventesimo secolo, nel
1905, ha smesso di
aggrapparsi al discontinuo ed è stato necessario
concepire uno
spazio non più piatto come nella geometria
euclidea, ma curvo [...]
la topologia, la cui dottrina fu enunciata da
Bernard Riemann,
diventava possibile; con essa venivano
finalmente concepite delle
realtà geometriche le cui proprietà potevano
sussistere dopo una
deformazione continua e venivano quindi liberate
della servitù delle misure e dei rapporti
quantitativi. La continuità prendeva
posto nel mondo, fino ad allora fisso della
geometria, in cui
l'avevano introdotta Eulero con i sette
ponti
e Möbius
con il suo nastro rimasto famoso. Questo stabiliva
la coesistenza e
la contraddizione di una forma definita, a due
facce, e del suo
percorso unitario nel tempo, percorso per il quale
non presentava che
una faccia» .
Pensare
liquido
Nell'
Enciclopedia
Treccani fra i neologismi compare la definizione di
“società
liquida”: «Concezione
sociologica
che considera l'esperienza individuale e le
relazioni
sociali segnate da caratteristiche e strutture che
si vanno
decomponendo e ricomponendo rapidamente, in modo
vacillante e
incerto, fluido e volatile» .
L'idea
di
modernità o società “liquida” è dovuta, come è
noto, a
Zygmunt Bauman
e rappresenta l'epoca del disimpegno,
dell'elusività,
dell'evasione facile e dell'inseguimento senza
speranza. In
questo tipo di società a dominare sono i più
elusivi, quelli liberi
di muoversi senza dare nell'occhio .
Si
arriva dunque al
nocciolo della questione: in una società che si
scioglie
inevitabilmente nel liquido, perdendo ogni punto di
riferimento
solido, caratterizzata da una marcata
individualizzazione del singolo
e da una incapacità di stare fermi in uno stato di
quiete, si apre
il sipario sull'architettura. “Ripensata”, come
aveva auspicato
Zevi, secondo lo stesso infatti «Nel
corso
dei secoli, una sola lingua architettonica è stata
codificata:
quella del classicismo ».
La
prima definizione
di “architettura liquida” giunge nel 1993 da parte
di Markos
Novak, «un'icastica
chiave
di lettura della contemporaneità nella sua accezione
di
multiforme determinazione dal virtuale al reale» .
L'architettura
liquida
in questo conteso veniva indissolubilmente legata al
cyber-spazio, che permette attraverso sistemi
software di rielaborare
forme architettoniche complesse, rendendole duttili
e malleabili,
dunque liquide. Le figure generate digitalmente
vengono completamente
manipolate dai progettisti, ridisegnati secondo la
natura formale e
la plasticità del contesto. Il cyber-spazio apre a
un nuovo
universo, realtà virtuale, multidimensionale, creata
attraverso le
reti della comunicazione globale. Un universo in cui
mancano vincoli
propri dello spazio e del tempo, un universo non
inerziale .
Novak scrive:
Una
architettura
liquida nel ciberspazio è chiaramente
un'architettura
smaterializzata, un'architettura che non si
accontenta più solo
dello spazio, della forma e della luce, e di tutti
gli aspetti del
mondo reale. È un'architettura di relazioni mutevoli
tra elementi
astratti» .
Dove
trovare allora i
germi di questo linguaggio liquido
nell'architettura? Arriva
prontamente la risposta di Stefano Colonna, il quale
fa derivare il
concetto di “liquido” dall' “anticlassico” di
arganiana
memoria. Nel saggio del 1930 Giulio Carlo Argan
coglie quelli che
Milizia considerava come errori nell'architettura
palladiana, come
germi, appunto, del codice anticlassico. Definizione
oggetto di
un'importante monografia dello stesso Argan: Classico
anticlassico:
il Rinascimento da Brunelleschi a Bruegel edita
a
Milano da Feltrinelli nel 1984. Da qui si sviluppa
il pensiero di
Zevi, che con toni provocatori, «riflette
sul
valore politico dell'anticlassico inteso come
rifiuto degli
schemi obbligatori imposti dalle dittature nei
termini di cogente
simmetria e parallelismi architettonici di natura
claustrofobica» .
Colonna si spinge oltre dopo aver
individuato una genesi
per l'architettura liquida, prova ad interpretarla,
offrendo
quattro chiavi ermeneutiche che possano offrire un
sistema per la
classificazione dell'architettura stessa.
Gli elementi che Colonna individua sono
quattro e
possono così riassumersi:
-
Labirinti
-
Frattali
-
Specchi
-
Mostri
Proviamo ora a fare luce su ogni chiave
ermeneutica,
fornendo gli adeguati esempi, affinché il nostro non
resti un
discorso teorico.
Labirinti.
L'archetipo del labirinto ha un riscontro in gran
parte della
storia dell'uomo e in tutta la sua produzione
artistica. Anche
quando ci sono stati mutamenti di gusto e di
indirizzo culturale, il
labirinto è sopravvissuto mutando senza estinguersi,
proprio come
certi organismi viventi, adattandosi alle nuove
condizioni, assumendo
nuovi messaggi e connotazioni .
Esiste
un legame
ancestrale tra l'architetto e il labirinto, un
legame articolato e
arduo da decifrare e classificare. Se, come ha detto
Bruno Zevi,
l'architettura è soprattutto una questione di
“spazio interno”,
allora il labirinto è l'essenza stessa
dell'architettura, il
sogno proibito dell'edificio, una forma di complesso
edipico che
l'architetto instaura col mito. Il labirinto entra
prepotentemente,
in quanto archetipo, nei disegni e nei discorsi
degli architetti, in
quel complesso circuito produttivo di immagini e
significati volti a
interpretare e trasformare l'ambiente .
Il
labirinto nel
contesto dell'architettura liquida serve
all'architetto come
“elemento di messa a sistema”, vale dunque come
sistema
teleologico, ovvero finalistico, che si avvale a sua
volta di sistemi
scientificamente fondati per arrivare a muovere gli
affetti dello
spettatore in maniera estetico-percettiva .
Frank
O. Gehry
lo
utilizza nel momento così drammatico di
contrapposizione fra le
“monadi architettoniche” nel Guggenheim
Museum
di
Bilbao.
Lo sguardo dello spettatore si inserisce tra gli
elementi che
compongono l'architettura nel suo insieme ed è
costretto a fare
continui cambi di visione a causa del moltiplicarsi
dei punti di
illuminazione, per via dello sfaccettamento delle
superfici e del
conseguente assommarsi di diversi livelli di
chiaroscuro che invitano
l'occhio ad una continua ridefinizione del punto di
inquadratura,
come se fosse impossibile mettere a fuoco solo su
una parte. Si può
affermare con certezza inoltre che lo studio per la
costruzione di
monadi in contrasto operata da Gehry a Bilbao sia
stata ispirata da
studi sulla cinetica e l'ottica, l'idro e
l'aereodinamica .
 Fig. 5 - Frank O. Gehry, Guggenheim Museum, Bilbao, 1997
Fig. 5 - Frank O. Gehry, Guggenheim Museum, Bilbao, 1997
Frattali.
La
parola
frattale è un neologismo coniato da Benoit
Mandelbrot nel
1970 che deriva dal latino fractus,
che significa interrotto, irregolare. La geometria
frattale è nata
agli inizi del XX secolo grazie agli studi di Gaston
Julia e ha
trovato il massimo sviluppo con l'avvento degli
elaboratori
elettronici che hanno permesso la visualizzazione
delle curve e degli
insiemi frattali. La geometria frattale aiuta a
comprendere le forme
presenti in natura. Queste forme presentano infatti
delle
ramificazioni, delle irregolarità, delle
frastagliature, delle
ripetizioni della forma su diverse scale .
La
geometria
frattale è presente ad esempio nelle felci, nei rami
di
pino e ginepro. In essi è evidente sia
l'irregolarità che
l'autosomiglianza. Nel corpo umano strutture
riconducibili ai
frattali sono osservabili nei neuroni, nelle fibre
nervose, nel
muscolo cardiaco, nei vasi sanguigni, nell'albero
bronchiale .
Questa
irregolarità,
questo frastagliamento richiama senz'altro l'idea
di caos,
che secondo gli antichi sarebbe una confusione
originaria della
materia informe, prima che il mondo sia ordinato .
L'esempio
più
convincente di utilizzo di geometria frattale
nell'architettura
liquida è il National
Museum
of Qatar
di Jean
Nouvel,
dove oltre al rimando alle geometrie tipiche del
minerale locale, la
cosiddetta “rosa dei venti” , si può notare la
volontà di
costruire forme complesse derivanti
dall'intersezione di corpi
solidi di forma irregolare. I corpi solidi costruiti
da Nouvel sono
così complessi che è stato particolarmente difficili
reinterpretarli con gli strumenti CAD esistenti e si
è dovuto
ricorrere a sofisticate implementazioni ed
aggiornamenti del
software .
Il
progetto
di Nouvel, inoltre, risulta complesso anche da un
punto di
vista ideologico, fondendo sia le componenti
indigene del Qatar,
ovvero quegli elementi identificativi che devono far
sentire ciascun
abitante dello Stato arabo in casa propria nel
momento della visione,
sia le componenti della cultura figurativa europea anticlassica
dell'arte del XX secolo .
Risponde
perfettamente
alle architetture
liquide
descritte da Marcos Novak, essendo infatti un
edificio di scultura
digitale, nato nel contesto del frenetico spazio
contemporaneo “cyber
spaziale”
.
 Fig. 6 - Jean Nouvel, National Museum of Qatar, Doha 2010
Fig. 6 - Jean Nouvel, National Museum of Qatar, Doha 2010
Specchi.
Nella teoria di Lacan, “Lo Stadio dello Specchio ”
è possibile comprendere il significato che lo
psicoanalista
attribuisce all'immagine riflessa nello specchio,
che definisce la
costituzione del punto in cui si genera l'io ,
la coscienza di sé e la costituzione del soggetto.
Avviene quindi,
l'identificazione di un io, e un riconoscimento che
porta allo
sdoppiamento tra soggetto reale e la sua immagine
ideale .
Sdoppiamento e quindi “doppio”, l'aspetto che a noi
maggiormente interessa in riferimento
all'architettura liquida,
perché proprio nella veste del duplice è affrontato
il tema dello
specchio. Si guardi l'opera Rem
Koolhaas
nell' Ampliamento
del
Museo Nazionale delle Belle Arti in Québec,
architettura del 2013. La scelta del tema dello
specchio in Koolhaas
deriva da un'oculata riflessione sulle teorie
concettuali di
Michelangelo Pistoletto, Daniel Buren e Bertrand
Lavier, tutti
artisti che si sono cimentati sul tema dello
specchio in chiave
concettuale.
Ad
esempio,
per Pistoletto, lo specchio rappresenta la metafora
della
vita, è infatti un dispositivo assai comune che
riesce a tenere una
serie di contraddizioni: lo statico e il dinamico,
l'ordine e il
disordine, il costante e il mutevole, il visibile e
l'invisibile.
Ogni dispositivo, come scrive Deleuze, «è
una molteplicità nella quale operano tali processi
in divenire,
distinti da quelli che operano in un altro» .
Ancora
l'opera
di Koolhas trova un confronto convincente in Côte
à
côte (2008)
di
Daniel Buren, oppure Bagatelle
(1990) di Bertrand Lavier .
In
questo
senso il tema dello specchio nell'architettura
liquida deve
molto agli studi della psicologia contemporanea
sulla formazione
dialettica dell'io. L'architettura di Koolhaas
possiede la
capacità di far interagire gli spazî
interni con gli spazî
esterni tramite un uso sapiente e ponderato delle
proprietà
opacizzanti e riflettenti del vetro. Risulta infatti
importantissima
la ricchezza delle modalità di fruizione
dell'edificio liquido
durante le varie fasce orarie diurne e notturne, e
sotto le
conseguenti e diverse fasi di illuminazione naturale
ed artificiale.
Inoltre lo sfruttamento delle trasparenze, lucide o
opache che siano
delle superfici perimetrali permette l'attivazione
psichica di
significati nascosti, appositamente studiata per
fornire
un'interpretazione profonda dell'oggetto museale il
quale,
interagendo intellettualmente con il fruitore,
diventa a sua volta
soggetto mitopoietico che riesce ad intercettare le
istanze culturali
del nuovo spettatore liquido .
 Fig. 7 - Rem Koolhaas, Ampliamento del Museo Nazionale
Fig. 7 - Rem Koolhaas, Ampliamento del Museo Nazionale
delle Belle Arti del Québec, Quebec City 2013
Mostri.
Il
mostro,
enigma che evoca mistero e stupore, perde, a
partire dal XIX
secolo, la sua meraviglia per acquisire un nuovo
significato e porsi
al centro dell'arte e delle speculazioni dei
filosofi della natura.
È
abbastanza insolito incontrare in un dipinto o
in una scultura
contemporanea l'aspetto di un corpo che rispetti
le leggi di
un'anatomia normale. Si prova quasi un distacco
imbarazzato nella
rappresentazione di un viso e nella
rappresentazione di un nudo che
obbediscano alle cosiddette regole accademiche.
Le forme mostruose
che l'arte contemporanea ostenta, saranno
considerate al contrario
come manifestazioni di un individuo liberato dai
suoi limiti, dalle
sue alienazioni, dalle sue conformazioni, o
persino come simbolo di
un'umanità svincolata finalmente dalle catene
della ragione e dei
canoni che reprimono la bellezza .
L'
“anomalia”
sarebbe soltanto una delle forme della
normalità,
forse la più ricca, la più avanzata. Essa
diviene in arte, come
nelle scienze della vita, l'elemento che sembra
spiegare per
contrasto, la formazione del “normale”
.
La
mostruosità
diviene l'oggetto di una scienza naturale in cui
il
mostro cessa di essere un oggetto particolare
per trasformarsi in un
soggetto comune d'esperienza.
Un
esempio
convincente dell'applicazione del tema del
“mostro”
nell'architettura liquida può essere il Kunsthaus
di
Graz,
realizzato dagli architetti Peter
Cook
e Colin
Fournier,
frutto
della
vittoria del concorso europeo del 1999 .
L'edificio si presenta come un «bozzolo
nodoso
ma allo stesso tempo dalla pelle liscia ».
Un mostro sì,
ma dalle sembianze di simpatico mostriciattolo,
tanto da vedergli
affibbiato il soprannome di “Friendly Alien”. La
forma biomorfica
del Kunsthaus presenta degli interessanti
precedenti nell'opera
dell'architetto, scenografo, artista e scultore
Frederik Kiessler.
Si rompe con il concetto classico dello spazio
cubico per trasformare
il suddetto spazio in un luogo aperto alla vita
ed eliminare
definitivamente la netta divisione fra
pavimento, pareti e soffitto
della scatola muraria. Vi
è
l'espressione di forze vitali intensificate fino
al punto di
un'intrinseca espansione, così guardando il
“Friendly Alien”
si ha l'impressione di vedere un organismo
vivente che respira e
sembra quasi che i suoi spazî
interni
vivano
di questi respiri e si modifichino in base alla
condizione
dell'organismo.
Organismo
che
in un certo senso riprende anche il Gaudì di
Barcellona, così
interessato agli esoscheletri di grandi
dimensioni in chiave
darwiniana .
 Fig. 8 - Peter Cook e Colin Fournier, Kunsthaus, Graz 2003, Quebec City 2013
Fig. 8 - Peter Cook e Colin Fournier, Kunsthaus, Graz 2003, Quebec City 2013
Le
tematiche
tuttavia, non sono sempre trattate
singolarmente, alcuni
temi possono incrociarsi, come il labirinto che
ben si abbina al
mostro, o lo stesso mostro che può abbinarsi al
“doppio” e
dunque allo specchio, ripercorrendo l'esperienza
di Giona.
Quello
che
tenteremo di dimostrare nelle prossime pagine è
quanto il nastro
di
Möbius
incarni perfettamente tutti e quattro i temi,
contemporaneamente, in
un continuo rimando. La topologia più in
generale, può offrire una
via all'architettura liquida?
Si
può
parlare di architettura topologica liquida?
Di
cosa
si occupa in sostanza la topologia? Si occupa di
studiare le
proprietà geometriche che rimangono invariate
quando le figure sono
sottoposte a trasformazioni continue, anche
quelle così profonde da
perdere tutte le proprietà metriche e
proiettive; ovvero le
proprietà topologiche sono proprietà che non
cambiano in seguito
alle trasformazioni geometriche più generali, ad
esempio quando si
sottopongono le figure a piegamenti o
stiramenti, senza però tagli o
strappi. Le figure geometriche conservano le
loro proprietà
qualitative.
La
topologia
è anche nota come “geometria del foglio di
gomma”
poiché ammette tutte le trasformazioni possibili
di una figura
disegnata su un foglio di gomma quando si
deforma a piacere, senza
strapparlo o lacerarlo .
La
nascita
ufficiale della Topologia avviene con la
pubblicazione nel
1895 del volume Analysis
Situs
scritto dal matematico francese Jules-Henri
Poincaré, nonostante il
termine sia in realtà utilizzato per la prima
volta nel 1847 da
Listing nel titolo del suo libro Vorsyudien
zur
Topologie
e problemi di topologia si possono trovare nei
lavori dei matematici
Leonardo Eulero, August Ferdinand Möbius e
George Cantor.
Verrebbe
da
chiedersi allora cosa hanno in comune la
geometria e
l'architettura essendo due discipline distinte e
autonome. La
geometria tuttavia, è una condizione necessaria
dell'architettura
in quanto tecnica di rappresentazione dello
spazio, strumento di
composizione architettonica ed anche valore
della struttura formale
del progetto. La geometria, nel suo carattere di
sistema
logico
è
strumento di definizione della configurazione
architettonica; essa
consente di disciplinare i processi creativi
innescati
dall'intuizione, dando all'architettura un
terreno di
razionalità .
L'assunzione
della
geometria topologica in alternativa alla
geometria euclidea si
basa sulla considerazione che quest'ultima sia
riduttiva e
fuorviante, essendo scienza delle figure più che
dello spazio .
Oggi
la
topologia esercita fascino e riscuote interesse su
vari architetti
proprio perché riguarda intuitivamente il concetto
di corpo
elastico, di corpo deformabile e perché implica la
dinamica della
forma, ovvero la sua variazione. A livello teoretico
l'applicazione
in architettura del punto di vista dinamico offerto
dalla topologia
cambia il modo tradizionale di concepire forme e
volumi: abbandonando
il mito della forma ideale, la forma viene intesa
dagli architetti
non in modo platonico cioè come un qualcosa di già
dato, di
preesistente, ma come il risultato di un'azione
dinamica di
trasformazione dalla quale essa scaturisce; si
tratta di un'idea di
forma plastica e flessibile continuamente
modificabile secondo una
variazione continua .
Oggi
nel
linguaggio architettonico si utilizza il termine
“liquido” in
riferimento ad una forma fluida, malleabile o anche,
in altri
termini, ad una massa informe. Ed ancora, la
conquista del volume
libero implica, poi, in architettura l'emancipazione
dallo spazio
consueto ortogonale in favore di uno spazio fluido,
differenziato,
continuo. Le deformazioni curvilinee delle superfici
avvengono come
si sa nel tempo, implicando oltre che una variazione
continua dello
spazio anche una variazione temporale e la
variazione
spazio-temporale in termini fisici significa
dinamismo, il che vuol
dire che il dinamismo è insito nelle forme stesse
che si inflettono
temporalmente. E allora, forte motivo di attrazione
da parte di
taluni architetti per la topologia è proprio l'idea
di spazio
topologico considerato nella sua accezione di spazio
dinamico, di
spazio-tempo. Le nozioni topologiche della
trasformazione e della
continuità si intrecciano con le tematiche
architettoniche della
flessibilità, della fluidità e del dinamismo .
Nelle
considerazioni
della Di Cristina si ritrovano tutti gli assiomi
fondamentali per la concezione di un'architettura
liquida. Si
“ritrova” il pensiero di Zevi che auspicava una
rottura con la
geometria euclidea e il suo collegamento
all'architettura classica
che per niente soddisfa le vere esigenze dell'uomo.
Si “rincontra”
Bauman, in quanto in una società così incline al
cambiamento, alla
trasformazione, anche l'architettura deve rispondere
a queste
condizioni, essendo essa stessa, “traduzione”, per
dirla alla
Rugino, di “momenti” significativi della storia
dell'uomo. Da
ultimo e non per ultimo si “ritrova” Novak, in
quanto avere
l'idea di una forma plastica continuamente
modificabile secondo una
variazione continua, è in linea con la sua
considerazione di
architettura nel Cyberspazio,
infatti
il
progettista non guarda all'oggetto in sé, ma alla
processualità
nella quale questo è inserito, con la sua genesi e
le sue successive
trasformazioni.
Continuità
e
discontinuità: Möbius
«In
quel
periodo provavo una strana avversione inesplicabile
per
l'abitare in cubi per superfici piane ed angoli, e
per le casse da
oggetti domestici, alias mobili. Nello svegliarmi e
nel fantasticare
il mio sguardo si rifiutava di essere ribaltato da
muri orizzontali e
verticali… cominciavo a progettare case nate dalle
mie
fantasticherie. Creazioni pazze tanto all'esterno
tanto all'interno
che però mantenevano sempre l'equilibrio statico,
malgrado la più
estrema dinamica» .
Con
queste
parole Hermann Finsterlin, esponente
dell'Espressionismo
tedesco, auspicava ben prima di Zevi, la nascita di
un'architettura
nuova, slegata da stilemi classici.
Parola
chiave
che si può dedurre dalle parole di Finsterlin è
dunque
“continuità”. In architettura la relazione di
continuità,
secondo l'interpretazione tradizionale, è essenziale
per le
configurazioni che rivelano una certa fusione degli
elementi-massa o
degli elementi spazio .
Considerando
però
l'ideale di continuità secondo un'ottica rovesciata
rispetto a quella tradizionale di cui sopra, le
forme plastiche della
curvatura ma anche della torsione e della piegatura,
riferibili alla
flessibilità della geometria topologica, sono capaci
di produrre
delle “differenziazioni” all'interno di un continuum.
La superficie topologica che si curva o si piega
sopra e in sé
stessa produce una “Variazione continua della
materia”; la
manipolazione progettuale del continuo determina una
distinzione di
zone spaziali senza che queste siano separate .
La
piega
è un continuum
topologico
che
Peter Eisenman ha teorizzato come tecnica
compositiva,
investigata poi da altri architetti come Greg Lynn,
Jeffrey Kipnis e
Bahram Shirdel. La piega produce la divisione
del
continuo.
La teoria della piega si richiama al concetto
leibniziano di materia
intesa come esplosiva e continua e si fonda sulla
filosofia di Gilles
Deleuze, il quale asserisce che un corpo flessibile
o elastico ha
parti coesive che formano una piega, così che esse
non sono separate
in parti di parti, ma sono piuttosto divise
all'infinito.
L'Alteka
Office
Building
a Tokyo di Eisenman offre un esempio chiaro della
teoria della piega,
ma non solo, anche un primo significativo confronto
con Möbius.
Lo stesso architetto scrive «Supponiamo
per
un momento che l'architettura possa essere
concettualizzata,
con un nastro di Möbius,
come
continuità ininterrotta tra interno ed esterno.
Che effetto
avrebbe questo sulla visione? Gilles Deleuze ha
proposto tale tipo di
continuità con la sua idea di ripiegatura.
Per Deleuze, lo spazio ripiegato costruisce un
nuovo rapporto tra
orizzontale
e
verticale,
figura e piano, interno ed esterno»
L'idea
del
paradosso di Möbius, quello cioè di una
superficie con una sola
faccia, non orientabile e percorribile in modo
continuo, cosicché
non è più possibile definire se si tratti di un
interno o un
esterno, sembra aver ispirato Eisenman
nell'ideazione del Max
Reinhardt
Haus di
Berlino
del 1992.
 Fig. 9 - Peter Eisenman, Max Reinhardt Haus, Berlino 1992
Fig. 9 - Peter Eisenman, Max Reinhardt Haus, Berlino 1992
Un'architettura
che
letteralmente si ripiega su se stessa in modo da
configurare un
oggetto che assomiglia ad una sorta di versione
tridimensionale del
singolo nastro.
Interessanti
ai
fini del nostro discorso risultano essere i
tentativi di Frederik
Kiesler, che ancor prima rispetto ad Eisenman e
precisamente a inizio
degli anni Trenta, tenta di conformare lo spazio
domestico sulla base
della teoria del correalismo,
secondo la quale non esistono oggetti isolati,
ma tutto è connesso
con tutto. Lo stesso Kiesler definisce il
correalismo come una
ricerca delle leggi di relazioni fra organismi
naturali e
artificiali. Nell'Endless
House
degli anni quaranta, primi anni cinquanta,
Kiesler articola lo spazio
secondo una forma quadrilobata che è il prodotto
della piegatura di
un nastro continuo, una sorta di nastro di
Möbius che mette in
stretto rapporto interno ed esterno, rendendo
esperibile e tangibile
il concetto di infinito .
Fino
a
qualche anno fa, questi erano progetti utopici, e
molti lo sono
ancora; gli architetti si divertivano a disegnare
progetti.
Irrealizzabili, quando non impensabili .
Non
impensabili,
questo è il tratto fondamentale. Ciò che si vuole
dimostrare infatti, è che senza la topologia,
sarebbe difficile
riuscire a parlare di architettura fluida.
Nuove
tecnologie
digitali, nuove tecniche costruttive, unite
all'utilizzazione in architettura di nuove forme
mutuate dagli
ultimi studi della matematica moderna e
contemporanea, hanno
profondamente mutato l'idea stessa di architettura.
Möbius
nelle
architetture liquide
 Fig. 10 - Friederik Kiesler, Endless House, 1958-59
Fig. 10 - Friederik Kiesler, Endless House, 1958-59
Il
loop
infinito del nastro di Möbius ha ispirato la
letteratura,
l'arte, la scienza. Ma come si pone in relazione
all'architettura?
L'architettura è qualcosa di più complesso, in
quanto deve
soddisfare anche un'esigenza pratica, che sia quella
dell'abitare,
dell'esporre, del vivere; può essere fruita
attraverso gli occhi,
ma anche attraverso gli altri sensi. «Ha
cura
delle cose mortali e sollecitudine per le terrene e
non ha nulla
a che vedere con gli dèi del cielo»
così si legge nel De
nuptiis
Philologiae et Mercurii,
un'operetta enciclopedica e didattica scritta nel V
secolo a. C. da
Marziano Cappella dove l'architettura e la medicina
vengono escluse
dalle arti liberali, poiché prime discipline che la
cultura
occidentale ha riconosciuto come moderne, in quanto
sottoposte
unicamente al vaglio di una razionalità che non ha
alcunché di
trascendente, ma che si fonda su una logica del
tutto terrena .
La
valenza
simbolica del nastro di Möbius, come abbiamo
osservato in
precedenza, è molto forte. È possibile dunque
trovare Möbius in
architetture fluide, ma ancor più nel dettaglio, può
essere una
chiave ermeneutica (ancor di più la topologia in
generale) per la
comprensione dell'architettura liquida?
Per
rispondere
a questi interrogativi, si propongono degli esempi.
Si
consideri la Möbius
House
di UNstudio come capostipite di una serie di
progetti in cui la
fluidità non è solo interna al progetto, ma si può
riscontrare a
livello concettuale anche sulla scala
interprogettuale.
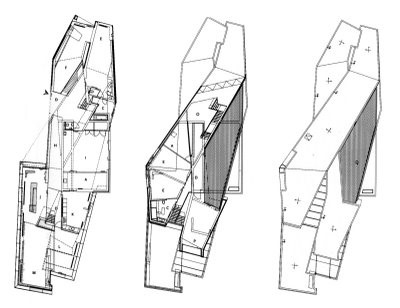 Fig. 11 - Ben Van Berkel, Casa Moebius (progetto), 1993
Fig. 11 - Ben Van Berkel, Casa Moebius (progetto), 1993
La
casa
a Het Gooi (1993-1999) prende forma sulla base di un
diagramma
determinato dal famoso anello di Möbius: una linea
continua a forma
di infinito in cui le due parti, che in questo caso
rappresentano una
coppia di intellettuali che hanno ampie sfere di
autonomia personale,
sono in alcune zone indipendenti in altre
intrecciate. Il progetto
viene risolto attraverso l'atto di avvolgere su se
stesso un
nastro.
Il
progetto
della Möbius House nasce dal voler integrare il
programma e
gli spazî
di una residenza privata con un paesaggio vario e
ricco .
Gli
architetti
Ben van Berkel e Caroline Bos di UNStudio
discutono
l'impatto sull'architettura delle nuove scoperte
scientifiche. Le
scoperte scientifiche hanno radicalmente
cambiato la definizione del
termine “spazio” attribuendogli una forma
topologica. Anziché
come modello statico di elementi costitutivi, si
percepisce lo spazio
come qualcosa di malleabile, mutevole, e la sua
organizzazione, la
sua ripartizione, la sua appropriazione
diventano elastiche. La casa
di Van Berkel ispirata al nastro di Möbius
è pensata come una struttura programmaticamente
continua, che
integra il continuo mutamento di coppie
dialettiche scorrevoli che
fluiscono l'una nell'altra, dall'interno
all'esterno, dalle attività
di lavoro a quelle del tempo libero, dalla
struttura portante alla
struttura non portante .
Il
tema
conduttore della Möbius
House
è il movimento e il nastro di Möbius ne è il
principio ordinatore.
Alla base vi è lo studio sulle diverse modalità di
fruizione dello
spazio domestico durante una giornata-tipo dei
committenti, che
essendo due entità, si muovono ognuna sulla propria
traiettoria, ma
condividono alcuni momenti di vita. Essendo la
rappresentazione
grafica di una giornata di vita familiare, il
diagramma ha una
dimensione spazio-temporale su cui sono trasposti
due diversi modi di
percorrere la casa. Le due orbite si intersecano e
compenetrano in
alcuni punti demarcando i momenti di condivisione
del tempo e dello
spazio e si allontanano in altri. Alle diverse parti
del nastro sono
associate le azioni che ognuno dei due utenti
svolge, separatamente o
insieme, all'interno della casa. Diverse zone del
nastro
rappresentano i luoghi deputati al sonno, al lavoro
e al soggiorno di
ognuno dei due occupanti: muovendosi lungo il nastro
si susseguono le
varie attività in un continuum spaziale.
All'interno
di
questa struttura unica, gli ambienti sono
predisposti per le
diverse funzioni, ma possono venir utilizzati in
maniera flessibile,
infatti lo spazio della casa non è suddiviso e gli
ambienti si
susseguono in maniera sequenziale e fluida. Le
distinte aree di
lavoro dei due padroni di casa sono inserite
all'interno degli altri
spazî
abitativi senza soluzione di continuità. Le diciture
classiche di
camera da letto, soggiorno o studio, vengono
sostituite dalle
espressioni sleeping,
living,
working,
a sottolineare l'azione che vi si svolge. Il nastro
di Möbius si è
così trasformato in un modello spaziale e poi
trasposto in forma
architettonica.
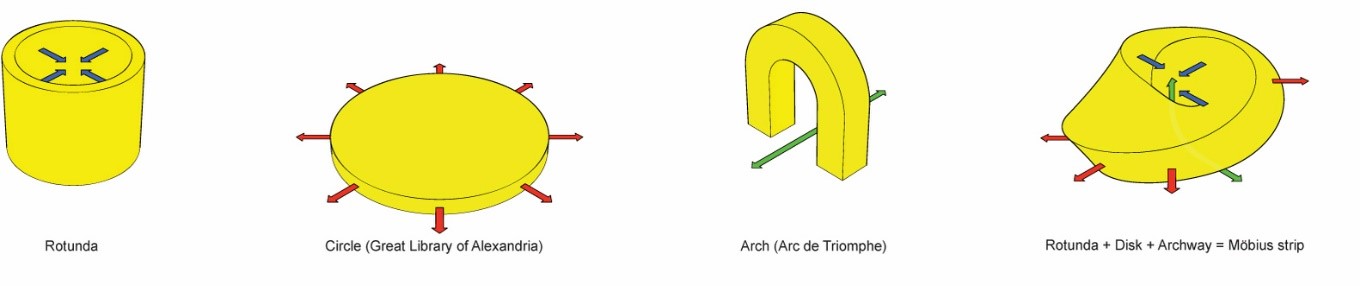 Fig. 12 - La rotonda, il cerchio e l'arco come elementi costituitivi
Fig. 12 - La rotonda, il cerchio e l'arco come elementi costituitivi
della struttura a nastro di Möbius
Progetto per la National Library, Astana, Kazakistan, 2009
 Fig. 13 - Big (Bjarke Ingels Group), Progetto per la Biblioteca nazionale, Astana, 2009
Fig. 13 - Big (Bjarke Ingels Group), Progetto per la Biblioteca nazionale, Astana, 2009
Il
progetto
di BIG (Bjarke Ingels Group) per la Biblioteca
Nazionale di
Astana in Kazakistan è anch'esso significativo ai
fini della
nostra ricerca. Su una superficie di circa 33'000 mq
si inserisce un
gigantesco nastro di Möbius, come intersezione di
due forme
principali: il cerchio e la spirale.
L'organizzazione razionale e
lineare della biblioteca è unita al loop
dell'infinito.
Nelle
volontà
dei progettisti vengono combinati quattro
archetipi:
-
Il
cerchio, che vuole riprendere l'antica
biblioteca d'Alessandria
-
La
rotonda
-
L'arco
di trionfo
-
La
Yurta, tipica abitazione della popolazione
nomade asiatica
Il
puro
diagramma del cerchio combinato con un percorso
“serpeggiante”
crea un'istituzione che è rigorosa, ma al tempo
stesso giocosa,
circondata da un parco che vuole essere
“libreria vivente” di
alberi, minerali e rocce, per permettere
ai visitatori di conoscere il territorio kazako
dalla città di
Almaty fino ad Astana.
Il
volume
si compone di una struttura circolare, ben
illuminata ed
ariosa, ospitante le biblioteche, e di una serie di
edifici pubblici
che avvolgono l'anello circolare delle biblioteche,
dall'interno
all'esterno, dal basso verso l'alto, offrendo viste
suggestive
sul paesaggio circostante e sullo skyline
cittadino.
La
relazione
tra le strutture interdipendenti (il cerchio
perfetto delle
biblioteche e la spirale degli edifici pubblici) dà
vita a un
edificio che adotta contemporaneamente
un'organizzazione
orizzontale, dove biblioteca, museo e attività di
supporto sono
collocati uno accanto all'altro, ed
un'organizzazione verticale, in
cui le funzioni sono impilate l'una sull'altra.
La “pelle”
della struttura costituisce il terzo elemento
significativo del
progetto: l'involucro cinge con andamento diagonale
e continuo i
due elementi architettonici della composizione
(cerchio e spirale) e
mette in relazione gerarchia verticale e
connettività orizzontale.
Il
nucleo
circolare interno contenente le collezioni della
Biblioteca
presidenziale è suddiviso in 42 partizioni
corrispondenti al numero
di lettere dell'alfabeto cirillico kazako. I tre
ponti principali del
cilindro sono, in linea di principio, uno spazio
integrato con
circolazione interna che consente un accesso
continuo e intuitivo a
tutti i supporti memorizzati. Aperta a qualsiasi
organizzazione:
alfabetica, cronologica o decimale la libreria
circolare coniuga la
massima flessibilità con la massima accessibilità.
Su
tutti
i lati, dentro e fuori, l'archivio circolare si
interseca con
gli spazî
comuni, le sale di lettura, le sale studio, gli
auditorium, il museo
e l'amministrazione, rendendo la biblioteca il cuore
programmatico
oltre che spaziale dell'istituzione.
La
spirale
ad anello invece è divisa in due sistemi separati.
Una
traiettoria continua di servizi e sale aggiuntive
come auditorium,
sale di lettura, strutture di ricerca, uffici
amministrativi, sale
riunioni e piccole conferenze, una sezione VIP e la
sede
presidenziale. La spirale intrecciata consente
inoltre un auditorium
dal soffitto doppio e strutture per conferenze. La
struttura a
gradini della spirale circolare offre condizioni
ottimali per gli
auditorium grazie alla pendenza e combina la
chiarezza continua con
la variazione spaziale.
Un
percorso
pubblico corre lungo la spirale circolare dal basso
verso
l'alto dell'edificio circoscrivendo il nucleo
cilindrico dentro e
fuori, trasformando il vuoto del sistema a doppia
facciata in un
atrio continuo che collega visivamente e
spazialmente tutti i
livelli.
Le
piastrelle
fotovoltaiche sulla facciata assorbono l'energia dal
sole
fornendo allo stesso tempo un'ombreggiatura passiva.
Inoltre, l'aria
circola naturalmente tra lo spazio interno della
struttura interna e
la zona di comfort climatico naturalmente regolata
dell'atrio.
La
Biblioteca
nazionale dei manufatti culturali si trova in una
biblioteca biologica vivente e geografica dei
paesaggi del
Kazakistan. Una sezione trasversale del terreno
kazako da sud a nord,
che collega Almaty e Astana, costituisce
l'ambientazione
dell'edificio. La vegetazione e gli elementi
topografici diversi che
vanno dalla regione dei monti Altai, al deserto di
Betpak-Dala e al
lago Balkhash a sud, alle steppe di Sary-Arka e alle
foreste di
conifere a nord sono distribuiti intorno alla
Biblioteca in uno
schema radiale. I percorsi di circolazione sono
strategicamente
intrecciati dappertutto per consentire l'accesso
pedonale da tutti i
bordi del sito, fornendo anche a ogni visitatore,
sia che arrivi a
piedi o in auto, un'esposizione completa alla
diversità del
paesaggio. Il terreno montuoso ridimensionato è
integrato nella base
dell'edificio creando un canyon naturale che
consente l'accesso sotto
la facciata a sbalzo. Un visitatore che fa un tour
della Biblioteca
Nazionale non solo sperimenterà la collezione
presidenziale e
otterrà un panorama prominente della nuova capitale,
ma acquisirà
anche un'idea della gamma del paesaggio, della flora
e della fauna
kazaka.
«L'edificio
della
Biblioteca Nazionale trascende le tradizionali
categorie
architettoniche come pareti e il tetto. Come una
yurta il muro
diventa il tetto, che diventa pavimento, che diventa
il muro di
nuovo»,
ha affermato Thomas Christoffersen, capogruppo del
progetto firmato
BIG .
 Fig. 14 - Vincent Callebaut, Swallow's Nest, Taichung, 2013
Fig. 14 - Vincent Callebaut, Swallow's Nest, Taichung, 2013
 Fig. 15 - Vincent Callebaut, Swallow's Nest, Taichung 2013
Fig. 15 - Vincent Callebaut, Swallow's Nest, Taichung 2013
Lo
Swallow's
Nest è la proposta spettacolare dello studio Vincent
Callebaut
Architectures,
per il futuro centro culturale, situato nel nuovo
"Gateway Park"
che si trova sul sito del vecchio aeroporto della
città di Taichung,
a Taiwan. Lo studio propone una “bioarchitettura”,
come afferma
lo stesso Vincent Callebaut infatti: «Si
deve
assistere ad una nuova convergenza tra mondo vivente
e mondo
della tecnologia per dare avvio a una trasformazione
di alchimie
complesse. Questa trasformazione spinge l'architetto
a diventare
savant-adventurer,
un
saggio
avventuriero. L'uomo ha costruito architettura per
proteggersi dalla natura distanziandosi sempre più
da essa. È
giunto il momento di riconciliarsi con essa» .
L'ambiziosa
architettura
organica, presa ora in considerazione procede da una
geometria rigorosa e complessa. Callebaut con questo
edificio
sperimenta con forme matematiche e geometrie
complesse. La pianta dei
vari piani si sviluppa attraverso la ripetizione
dell'anello di
Möbius per ben 8 volte, ogni volta incrementando
l'angolazione di
45 gradi per compiere un'intera rivoluzione intorno
all'asse
centrale costituito dal largo patio della
costruzione. Queste spirali
orizzontali formano tre volumi che svettano,
liberando il passaggio
sotto di esse, accogliendo i visitatori e
direzionando i flussi dei
passanti. La pianta è infatti studiata per agevolare
l'accesso tra
le due aree residenziali di Gateway Park. Il cortile
dà l'illusione
di una forma infinita, illusoria, esattamente come
l'anello di
Möbius deve perdersi con lo sguardo ingannato dalle
forme delle
facciate che si riflettono sul giardino acquatico
con un gioco di
specchi infiniti. Sostando nel patio lo sguardo del
visitatore si
apre da entrambi i lati sul verde di Gateway Park.
L'ampia piazza
offre un riparo piacevole per gli spettatori del
teatro con la
biglietteria, il bar e i negozi sapientemente
inglobati nella
struttura, mentre un parco di sculture caratterizza
il paesaggio
esterno.
L'edificio
si
appoggia su tre gruppi di pilastri che sorreggono la
struttura e
la innalzano dal terreno, e che fungono da spazî
per i flussi verticali. Queste torri sono ricoperte
da vegetazione in
modo da creare giardini verticali interni che
servono sia per il
raffrescamento sia come decorazione (impossibile che
l'architetto
rinunci al verde in una sua opera). All'interno si
prediligono la
luminosità, le forme sinuose e colori chiari. I
piani sono aperti su
tutti i lati, sia nel patio interno sia verso la
città. Callebaut
gioca tutto sulla trasparenza aumentando l'effetto
di
spettacolarità dell'edificio. Le facciate
intelligenti, ricoperti
di vetri e-low
e “pixellate” con celle fotovoltaiche per garantire
una quantità
di approvvigionamento elettrico, controllano
l'accesso della luce
naturale. Allo stesso modo le celle servono per
assicurare una
facciata oscurata e possono essere disposte
strategicamente per
tutelare opere e spazî
nell'area museale, oppure fornire ombra dove la
superficie della
finestra è pressoché orizzontale .
I
tre pilastri principali sopportano tre enormi volte,
che ospitano gli
spazî
espositivi delle opere d'arte del museo e della
biblioteca, veri e
propri hub di connessione tra il patio centrale e il
centro
culturale, la città e il parco. Risultato? Questo concept
strutturale permette di liberare completamente il
suolo,
trasformandolo in un immenso giardino acquatico e
floreale.
I
pavimenti sono attraversati da strutture verdi: tre
giardini
verticali che accolgono i visitatori dall'agora
centrale. Le pareti di vetro d'e-low
glass intelligenti, che integrano mini celle
fotovoltaiche, vantano
effetti di traslucidità progressiva e un alto tasso
d'isolazione
termica: l'edificio è previsto ad emissione zero.
Questo nido di
rondine votato alla biodiversità, vuole essere un
progetto
pionieristico che simboleggia l'armonia della
scienza e della
natura. «Ideato
all'immagine
del nastro di Möbius, è un centro culturale senza
fine, che interrogherà, intrigherà e sveglierà i
neuroni dei suoi
visitatori»
spiega il belga Vincent Callebaut, architetto
visionario, noto per i
suoi progetti futuristici, come ad esempio Dragonfly,
una
fattoria a New York,
pubblicata da Futurix nel 2009.
Ci
si
è voluti soffermare solo su alcuni esempi in cui
il riferimento a
Möbius
è
davvero evidente, in quanto, dà forma
all'architettura,
tuttavia in molte opere di Frank O. Gehry o di Zaha
Hadid è
impossibile non cogliere un riferimento alla
topologia e più in
particolare a Möbius stesso, magari “nascosto” tra
volumi
sinuosi.
Si
ricordi
infatti che per la sezione Istallazioni della
Biennale di
Architettura di Venezia del 2008 fu presentato il
progetto di Zaha
Hadid e Patrick Schumacher, Lotus,
diviso tra una sala delle Corderie e i saloni di
Villa Malcontenta,
una delle costruzioni più famose del Palladio, sul
fiume Brenta,
lontano da Venezia. Partendo dalle rigide
proporzioni geometriche
della villa palladiana, mediante un algoritmo
matematico, sono state
realizzate forme che «nel mezzo dell'ambiente
edificato
esistente», sia nella sala delle Corderie sia nella
villa,
propongono «un sistema di arredi racchiusi tramite
cui sedurre e
catturare il mondo immediato e quello più distante».
Modificando,
trasformando le regole, «anziché rappresentare un
sistema già
addomesticato di norme interne, la sala Lotus
seduce attraverso le pieghe dal ritmo ondulato, le
sue esclusioni, la
sua riconfigurabilità e la sua capacità di restare
al di fuori
delle categorie .
Il riferimento a Möbius è particolarmente
significativo.
Di
nuovo
un continuo rimando come in un nastro di Möbius,
dall'anticlassico di Palladio, si arriva al liquido,
l'installazione si scioglie nell'ambiente occupando
lo spazio in
maniera topologica.
 Fig. 16 - Zaha Hadid & Patrick Schumacher, Algorithm, project Lotus
Fig. 16 - Zaha Hadid & Patrick Schumacher, Algorithm, project Lotus
11.a Mostra Internazionale di Architettura, Venezia, 2008
Conclusioni
Ripercorrendo
la
storia del nastro di Möbius
è
stato così possibile comprenderlo fino in fondo,
dalla sua
scoperta, alla sua applicazione meccanica, dal suo
manifestarsi negli
oggetti di tutti i giorni, fino all'invisibilità
delle molecole,
che pur compongono il nostro mondo.
Una
figura
duplice, ambigua, che però può riuscire davvero a
rendere
omaggio pienamente all'architettura liquida.
Proponendola come
chiave ermeneutica, ci si rende conto di quanto sia
in fin dei conti
un riassunto delle precedenti chiavi ermeneutiche
già proposte
finora (labirinto, specchio, geometria frattale,
mostro).
Esprime
bene
la tematica del labirinto, un labirinto unicursale
in cui è
facile perdere l'orientamento, ben espresso ad
esempio nel film di
Gustavo Mosquera, in cui un convoglio della
metropolitana si disperde
nella nuova linea, che ha inconsapevolmente creato
un nastro di
Möbius, da cui i protagonisti non riescono ad
uscire.
Riprende
la
tematica dello specchio, nella sua accezione di
“doppio”, in
quanto la duplicità è la caratteristica chiave del
nastro, interno
ed esterno sono uniti in un inestricabile presente,
in quanto
superficie non orientabile, impossibili da
discernere.
Si
collega
alla geometria frattale, in quanto loop infinito, ma
anche
attraverso le trasformazioni di Möbius che oltre ad
essere
utilizzate in fisica e in matematica, possono essere
sfruttate per
produrre stupefacenti immagini artistiche di
frattali.
Infine
ben
si sposa con l'idea di mostro in quanto richiama
l'ancestrale
figura dell'ouroboros,
non è un caso se ad esempio una delle prime
rappresentazioni del
nastro sia proprio sotto forma di questo serpente
che si morde la
coda nella Chrysopoeia
di Cleopatra.
Dunque
è
possibile che in architettura le superfici
ordinarie cedano il
passo al nastro di Möbius:
un'unica superficie che diviene interno ed
esterno. Un solo lato e
un solo bordo, in un involucro fluido che piega
gli orizzonti in una
spazialità liquida. Lo spazio attraversabile
diviene una finestra
sulla piazza, punto di riflessione, ed
istantanea sugli orizzonti del
proprio tempo.
Con
questo
non si vuole dire che nella città del futuro saremo
circondati da nastri di Möbius ovunque e per
qualunque tipo di
edificio, ma che il nastro può offrire una via
all'architettura
liquida, in quanto contiene dentro di sé una nuova
concezione
spaziale, ma anche una nuova concezione geometrica,
a farla da
padrona è senza dubbio la topologia.
L'architettura
topologica
fluida è una realtà dei nostri tempi. Nuove
tecnologie
digitali, nuove tecniche costruttive, unite
all'utilizzazione in
architettura di nuove forme mutuate dagli ultimi
studî
della matematica moderna e contemporanea, hanno
profondamente mutato
l'idea stessa di architettura. Da sempre vi è stata
una grande
relazione tra la matematica e l'architettura,
dall'antica Grecia
ai tempi moderni. Le nuove idee di spazio e le nuove
geometrie hanno
contribuito a modellare l'idea di spazio in
architettura in maniera
completamente diversa. È una lunga storia che
continua. È una
tradizione radicata nella storia dell'architettura.
Dal punto di
vista del matematico è una questione di grande
interesse, anche se
magari tanti architetti, maggiormente legati alla
storia e alla
tradizione, pensano che la moderna architettura
fluida e topologica
non sia architettura. Dimenticando che il
tradizionale legame tra
matematica e architettura cambia come cambia la
matematica e l'idea
di spazio.
La
“fluidità”
è una delle parole chiave dell'architettura
contemporanea. E senza la topologia, la scienza
delle trasformazioni
continue, sarebbe stato difficile immaginare queste
nuove forme. Il
nastro di Möbius dunque offre l'esempio archetipo di
utilizzo
della topologia nell'architettura fluida.
Ciò
che
più interessa agli architetti che teorizzano sulla
logica della
curvilinearità e delle pieghe è il significato di
termini come
“evento”, “evoluzione” e “processo”, vale a dire,
del
dinamismo connaturato alle configurazioni fluide e
flessibili di ciò
che oggi si definisce “architettura topologica”. Per
“topologia
architettonica” si intende la variazione dinamica
della forma
agevolata dalle tecnologie digitali, dal CAD e dai software
di animazione. La topologizzazione della forma
architettonica secondo
configurazioni complesse e dinamiche porta il
progetto di
architettura verso una nuova e spesso spettacolare
plasticità, sulla
scia del Barocco e dell'Espressionismo organico. Ed
ecco cosa
intende per “topologia architettonica” uno dei più
interessanti
architetti “virtuali”, Stephen Perrella, scomparso
nel 2008: «La
topologia architettonica è la mutazione della forma,
della
struttura, del contesto e del programma in modelli
compositi e
dinamiche complesse. Negli ultimi anni, si è
sviluppata una
sensibilità progettuale grazie alla quale le
superfici
architettoniche e gli elementi topologizzanti della
forma vengono
esplorati in maniera sistematica e inclusi in
diversi programmi
architettonici. Influenzato dall'intrinseca
temporalità dei
software
di animazione, della augmented
reality,
della produzione industriale computerizzata e, in
generale,
dell'informatica, lo “spazio” topologico differisce
da quello
cartesiano perché in esso gli eventi temporali
diventano parte
integrante della forma. Lo spazio, dunque, non è più
un vuoto al
cui interno sono contenuti soggetti e oggetti; lo
spazio, invece, si
trasforma in una fitta e interconnessa rete di
particolarità e
singolarità che si potrebbe definire “materia” o
“spazio
pieno”»
. Osservazioni in cui confluiscono idee sulla
geometria, sulla
topologia, sulla computer
graphics,
sullo spazio–tempo, e si potrebbe continuare. Perché
i nessi, i
fili di Arianna della cultura nel corso degli anni
hanno funzionato:
nuove parole, nuovi significati, nuovi legami, nuove
influenze, nuove
forme, nuovi spazî.
In un processo senza fine. In cui le idee della
matematica sullo
spazio sono parte fondamentale.
NOTE
PICKOVER
2006, pp. 19-20


